Consultar y evidenciar lo consultado en su blog.
1. Características de un circuito serie.
2. Características de un circuito paralelo.
3. Como obtener el equivalente de dos resistores en serie.
4. Cómo obtener el equivalente de dos resistores en paralelo.
5. Cómo leer el código de colores de los resistores.
Respuestas:
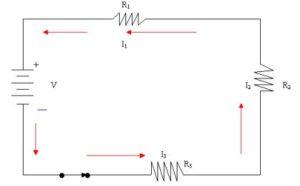
1. Un circuito en serie es aquel en el cual la conexión de los elementos se realiza uno seguido del otro; es decir, en secuencia. En estos circuitos la corriente eléctrica circula a través de un único camino, desde la fuente generadora de energía hacia los componentes que constituyen el ensamblaje (resistencia, condensadores, inductores, interruptores, etc.).
os circuitos en serie tienen una conexión general en secuencia. Esto les concede ciertas especificaciones técnicas, las cuales se detallan a continuación:
Los terminales de los elementos se conectan sucesivamente
El terminal de salida de un elemento (negativo) se une al terminal de entrada del siguiente componente (positivo).
El voltaje total es igual a la suma de los voltajes de los elementos individuales
En caso de que se cuente con solo una fuente de voltaje, entonces la tensión aplicada al sistema será igual a la suma de las caídas de tensión en cada elemento del circuito.
Así, la expresión matemática que se emplea para este fenómeno es la siguiente:
En el caso de la conexión de múltiples baterías, al conectar dos pilas el resultado obtenido es la suma de ambos voltajes.
Lo anterior ocurre siempre y cuando se conecten ambas fuentes de energía con la polaridad adecuada; esto es, el negativo de la primera pila con el positivo de la segunda pila, y así sucesivamente.
La intensidad de la corriente es la misma en cualquier punto del circuito en serie
Esto se debe a que la corriente no se divide en ninguna ramificación, ya que todo circula a través de una misma vía.
Esto se traduce en que misma intensidad de la corriente atraviesa a todos y cada uno de los elementos conectados en el montaje en serie.
La resistencia equivalente del circuito es la suma de todas las resistencias
Ya que la intensidad de la corriente sigue un solo camino de circulación, la resistencia total del circuito es igual a la suma de todas las resistencias que lo componen.
Matemáticamente, este principio se expresa de la siguiente forma:
Mientras más resistencias estén conectados al circuito, mayor será la resistencia total equivalente del sistema y, según la Ley de Ohm (V=I*R), si la resistencia aumenta, entonces la intensidad disminuye.
En síntesis, en tanto más resistencias conectemos al circuito en serie, menor será la corriente que circule a través de él.
Los componentes del circuito son dependientes entre sí
Por ejemplo, si el circuito incluye la conexión de algún interruptor y este se abre, automáticamente la corriente deja de circular a través del circuito, independientemente de cuál haya sido el punto de desconexión.
Lo mismo sucede si uno de los elementos se avería durante su operación. Si un componente se funde o se desconecta, entonces el circuito se abrirá en ese punto y la corriente dejará de circular.
Además, la naturaleza del circuito implica que todos los componentes se conectan o desconectan simultáneamente.
Es decir, o el circuito está abierto (y por ende, todos los componentes desconectados) o el circuito está cerrado (y en consecuencia, todos los componentes están conectados).
2. En un cirtuito de resistencias en paralelo podemos considerar las siguientes propiedades o características:
- La tensión es la misma en todos los puntos del circuito.
- A cada uno de los caminos que puede seguir la corriente eléctrica se le denomina "rama".
- La suma de las intensidades de rama es la intensidad total del circuito, coincide con la que sale de la pila. (Esta es una de las leyes de Kirchoff)
Donde IT es la intensidad total e Ii son las intensidades de rama.
- La inversa de la resistencia equivalente del circuito paralelo es igual a la suma de las inversas de las resistencias.
Donde Rp es la resistencia equivalente del circuito paralelo, y Ri son las distintas resistencias de rama.
Despejando en la expresión anterior obtenemos:
Si particularizamos para el caso de tener sólo dos resistencias:
- La resistencia equivalente es menor que la menor de las resistencias del circuito.
- Las intensidades de rama las calculamos con la Ley de Ohm.
Donde Ii es la intensidad de rama, VS es la tensión de la pila y Ri es la resistencia de rama.
Dadas estas características, decir que este circuito también recibe el nombre de divisor de intensidad.
Para simplificar el circuito, vamos aplicando las propiedades que hemos visto en el apartado anterior, veamoslo con un circuito de 2 resistencias:
El primer paso consiste en hallar la resistencia equivalente del circuito (Rp), y sustituir las 2 resistencias por la que hemos calculado
En este circuito simplificado podemos calcular el parámetro que nos falte, de los tres que intervienen.Consideremos los siguientes valores en el circuito de 2 resistencias del apartado anterior: VS = 12 v., R1 = 40 KW y R2 = 60 KW.Tenemos que calcular: Rp, IT, I1 e I2.- En primer lugar calculamos Rp: Rp = (R1·R2)/(R1+R2) = (40·60)/(40+60) = 24 KW.
- A continuación calculamos IT: IT = VS / Rp = 12 v/24 KW = 0'5 mA.
- Y seguidamente calculamos I1 e I2:
I1 = VS / R1 = 12 v/40 KW = 0'3 mA.
I2 = VS / R2 = 12 v/60 KW = 0'2 mA.
- También podríamos haber calculado IT como la suma de I1 e I2:
IT = I1 + I2 = 0'3+0'2 = 0'5 mA
3. Cuando en un circuito hay varias resistencias conectadas, resulta útil para calcular las corrientes que pasan por el circuito y las caídas de tensión que se producen, encontrar una resistencia que pueda sustituir a otras, de forma que el comportamiento del resto del circuito sea el mismo; o sea, debemos encontrar o calcular la Resistencia equivalente .
Esta resistencia equivalente, se sabe que existe, y para configuraciones en que las resistencias a sustituir están en paralelo o en serie, son fáciles de calcular como veremos más adelante.
En ocasiones encontrarás resistencias en circuitos que no se pueden considerar exclusivamente en paralelo ni en serie, como en el diagrama de abajo (diagrama 1).
Las reglas para encontrar resistencias equivalentes a otras, ya sea en paralelo o en serie, se pueden aplicar de forma reiterada. Por ejemplo, si la resistencia equivalente a dos resistencias conectadas en serie (en el diagrama 82 ohm y 68 ohm) se encuentra en paralelo con otras, nada impide encontrar una resistencia equivalente a las dos en serie y después repetir el proceso con las que se encuentran en paralelo.
4.
RESISTENCIAS EN PARALELO
Decimos que dos resistencias están en paralelo cuando los terminales de salida están unidos entre si al igual que los terminales de entrada.
CALCULO DE RESISTENCIAS EN PARALELO EQUIVALENTE
El circuito de la figura 1 se puede reemplazar por un único resistor, de esta manera reducimos el costo del circuito y la cantidad de componentes necesarios.
Para calcular la resistencia equivalente tenemos que hacer el siguiente calculo de la figura 2, esto es posible gracias a que en conexiones en paralelo la tensión entre sus terminales es la misma y mediante la ley de ohm se puede establecer esta relación.
La suma de las inversas de cada resistor en paralelo da como resultado la inversa de la resistencia equivalente, para finalmente encontrar el valor de la resistencia equivalente tenemos que despegar RE.
5.
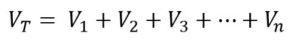
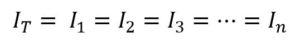
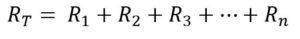
Comentarios
Publicar un comentario